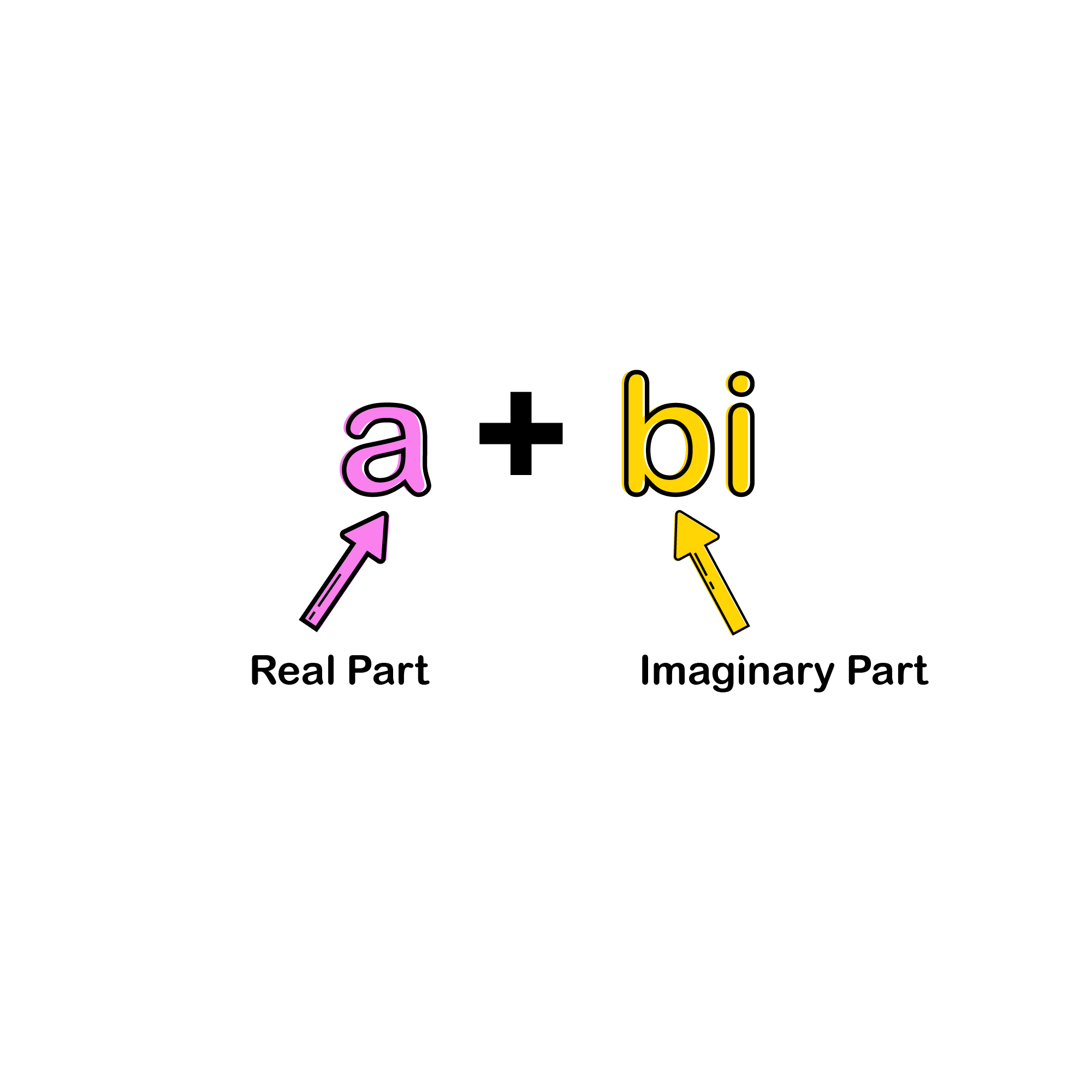
Complex Numbers
There is a new “number” that we associate negative numbers with under the square root. These are called COMPLEX NUMBERS, and they are indicated with the letter i, where: \(i=\sqrt{-1}\)
We can do regular operations like addition, subtraction, multiplication, and division with complex numbers. Keep the following in mind, to make complex multiplication simpler.
\(i=\sqrt{-1}\)
\(i^{2}=i\times i=\sqrt{-1}\times \sqrt{-1}=-1\)
\(i^{3}=i\times i\times i=\sqrt{-1}\times \sqrt{-1}\times \sqrt{-1}= -1\times \sqrt{-1}=-i\)
\(i^{4}=i^{2}\times i^{2}=-1\times -1=1\)
\(i^{5}=i^{4}\times i=i\)
\(i^{6}=i^{4}\times i^{2}=-1\)
\(i^{7}=i^{4}\times i^{3}=-i\)
\(i^{8}=i^{4}\times i^{4}=1\)
Solved Example 1
Find the value of \(i^{203}\)
A. i
B. -i
C. 1
D. -1
Solution: Now, we need to first break up \(i^{203}\: to\: i^{202+1}\)
\(i^{202}\times i^{1}\)
\((i^{2})^{101}\times i\)
\((-1)^{101}\times i\)
-1 x i
= -i
The correct answer is B.
Add and Subtract Complex Numbers
Adding and subtracting complex numbers is similar to adding and subtracting polynomials. Just add or subtract the real and imaginary parts.
Example: Solve: (-6 - 5i) - (3 - 4i)
(-6 - 5i) - (3 - 4i) = (-6 - 5i) + (-3 + 4i)
= [-6 + (-3)] + (-5 + 4)i
= -9 - i
Multiply Complex Numbers
Multiplying complex numbers is similar to multiplying polynomials.
Solve: (2 + 5i) (6 + 4i)
(2 + 5i) (6 + 4i) = 12 + 8i + 30i + 20i2
= 12 + 38i + 20(-1)
= 12 + 38i - 20
= -8 + 38i
Divide Complex Numbers
For complex division, we need to know what a conjugate is. For starters, all complex numbers take the form of a + bi, where a is the x-coordinate and b is the y-coordinate. A complex conjugate is changing the + in a + bi to a − bi or vice versa. When we have complex division, we multiply by a clever form of “one,” which will be the conjugate of the denominator.
Example: Write each quotient in the form \(a+bi:\frac{6}{7-4i}\)
\(\frac{6}{7-4i}=\frac{6}{7-4i}\times \frac{7+4i}{7+4i}\)
\(\frac{42+24i}{49-16i^{2}}\)
\(\frac{42+24i}{49-16(-1)}\)
\(\frac{42+24i}{65}\)
\(\frac{42}{65}+\frac{25}{65}i\)