Solid Geometry
SOLID GEOMETRY is the name for geometry performed in three dimensions. Instead of flat shapes like circles, squares, and triangles, solid geometry deals with spheres, cubes, and pyramids (along with any other three-dimensional shapes). And instead of using perimeter and area to measure flat shapes, solid geometry uses surface area and volume to measure its three dimensional shape.

The following are solid geometry shapes generally tested on the SAT:
1. Cubes
A CUBE is created by the connection of six square faces. The formula for the volume of a cube is as follows. Volume is a representation of the amount of space that the shape takes up. You can also think of it as the amount of liquid that could fill the three-dimensional shape.
\(V_{cube}=l\: w\: h=s^{3}\)
The surface area can be thought of as the wrapping around the object. In the case of the cube, the surface area is the sum of the area of the faces.
\(Surface\: Area=6s^{2}\)
Questions about cubes may also ask you to solve for lateral area (for example: how much space must be painted in a room for its walls to be repainted.) You just want to calculate the surface area of four sides.
\(Lateral\: Surface\: Area=4s^{2}\)
Solved Example 1
Johnny is painting a room in his house where the walls are all square. One wall takes roughly two gallons of paint and one gallon of paint covers 32 \(ft^{2}\). If there are four walls in the room that Johnny is painting, approximately how many square feet does he paint?
A. 216 \(ft^{2}\)
B. 224 \(ft^{2}\)
C. 256 \(ft^{2}\)
D. 264 \(ft^{2}\)
Solution: Putting words into equations,
1 gallon = 32 \(ft^{2}\)
1 wall = 2 gallons
Therefore, 1 wall = 2(32 \(ft^{2}\)) = 64 \(ft^{2}\)
Now, since there are four walls, the total square feet required is 4 x 64 = 256 \(ft^{2}\)
The correct answer is C.
Solved Example 2
What is the maximum number of rectangular blocks measuring 3 inches by 2 inches by 1 inch
that can be packed into a cube shaped box whose interiors measures 6 inches on an edge?
A. 24
B. 28
C. 30
D. 36
Solution: You're trying to fit smaller rectangles into a larger rectangle, so you're dealing with volume, not surface area. Find the volume of the larger rectangle (which in this case is a cube).
You can use the formula for the volume of a cube: \(s^{3}\rightarrow 6^{3}=216\)
Now find the volume of one of the smaller rectangular solids: LWH \(\Rightarrow (3)(2)(1)=6\)
And divide the larger rectangular solid by the smaller to find out how many of the smaller rectangular solids can fit inside the larger: \(\frac{216}{6}=36\)
The correct answer is D.
2. Cuboid or Rectangular Prism
The cuboid is often called a rectangular solid or a rectangular and triangular.
Volume = l w h
Surface Area = 2lw + 2lh + 2wh = 2(lw + lh + wh)
Lateral Surface Area = 2lh + 2wh = 2(lh + wh)
Solved Example 3
Sally has a fish tank shaped like a rectangular prism. It has a width that is three times its length and twice its height. If the tank is 75% full when holding 3375 /(cm^{3}\)
of water, what are the dimensions of the tank?
A. l = 10 cm, w = 30 cm, h = 15 cm
B. l = 12 cm, w = 36 cm, h = 12 cm
C. l = 8 cm, w = 24 cm, h = 15 cm
D. l = 15 cm, w = 15 cm, h = 25 cm
Solution: Since the tank is 75% full and the volume is 3375 /(cm^{3}\) when 75% full, the entire volume of the prism is = 4500 /(cm^{3}\)
Additionally, we are given that:
\(w=3l\rightarrow l=\frac{w}{3}\)
\(w=2h\rightarrow h=\frac{w}{2}\)
Therefore, V = l w h
\(4500=\frac{w}{3}\) x w x \(\frac{w}{2}=\frac{w^{3}}{6}\)
\(w^{3}=2700\)
w = 30
\(l=\frac{w}{3}=10\)
\(h=\frac{w}{2}=15\)
The correct answer is A.
3. Triangular Prisms
Triangular prisms are made up of nine lines and six vertices. They contain two triangular faces and three rectangular faces.
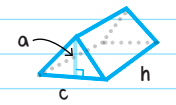
\(Volume=\frac{1}{2}a.c.h\)
a = height of the triangular base
c = side length of triangle
h = height of the prism
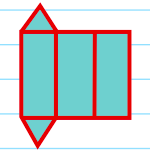
\(Surface\: Area=2(A_{1})+A_{11}+A_{12}+A_{13}\)
\(A_{1}\) = Area of the triangle faces
\(A_{11},A_{12}\: and\: A_{13} =\) the areas of each of the rectangular faces
Solved Example 4
Diane is creating a triangular prism and wants to know how many jelly beans can fill the object. The triangular base has a side length of 4 in and a height of 3 in. The height of the prism is 10 in and 20 jellybeans fill 25 /(in^{3}\) . Approximately how many jellybeans will fill the prism?
A. 48
B. 52
C. 60
D. 64
Solution: First, let's calculate the volume of the prism.
\(Volume=\frac{1}{2}\: a.c.h\: =\frac{1}{2}\: 4.3.10\: =60\: in^{3}\)
Knowing the volume of the prism, we can proceed to solve for how many jellybeans will fill it.
We know that 20 jelly beans fill 25 /(in^{3}\) of space, so we can set up a proportion to solve for how many jelly beans fill 60 /(in^{3}\) of space: \(\frac{20\: jelly\: beans}{25\: in^{3}}\) x \(\frac{x\: jelly\: beans}{60\: in^{3}}\)
x = 48 jellybeans
Approximately 48 jellybeans would fit in the prism described, so A is the correct answer.
4. Pyramids
There are two different types of pyramids determined by the shape of their base: triangular or square. For triangular base pyramids, the three-dimensional object is created by four triangular faces. Rectangular based pyramids are created from four triangular faces and one rectangular face.
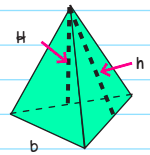
\(Volume=\frac{1}{3}Area(Base).H\)
Area = Area of the Base
H = height of the pyramid
Solved Example 5
Hannah has a die in the shape of a triangular pyramid. The side length of one of the triangular faces is 2 cm and its height is 1.732 cm. The height from the base of the pyramid to the top of the pyramid is 4 cm. How much volume does the die have?
A. 2.236 /(cm^{3}\)
B. 2.309 /(cm^{3}\)
C. 2.405 /(cm^{3}\)
D. 2.525 /(cm^{3}\)
Solution: The following information is given:
b = 2
h = 1.732
H = 4
\(Volume =\frac{1}{6}\cdot 2\cdot 1.732\cdot 4=2.309\: cm^{3}\)
The correct answer is B
5. Cylinders
In order to determine the surface area of a CYLINDER, sum the areas of the three surfaces: The area of each circle is \(\pi r^{2}\), while the area of the rectangle is length x width. Looking at the figures below, we can see that the length of the rectangle is equal to the circumference of the circle (2rπ), and the width of the rectangle is equal to the height of the cylinder. Therefore, the area of the rectangle is 2nr x h.
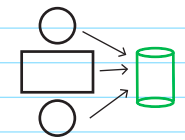
To find the total surface area of a cylinder, add the area of the circular top and bottom, as well as the area of the rectangle that wraps around the outside.
\(Area_{cylinder}=2\: Circles+1\: Rectangle=2(\pi r^{2})+2\pi rh\)
The volume of a cylinder measures how much “stuff” it can hold inside. In order to find the volume of a cylinder, use the following formula: \(Volume_{cylinder}=\pi r^{2}h\)
Solved Example 6
A can of peaches has a label that stretches all around it. If the height of the can is 5 inches and the length across the can is 3 inches what is the area of the label?
A. 8 π/\(in^{2}\)
B. 10 π/\(in^{2}\)
C. 12 π/\(in^{2}\)
D. 15 π/\(in^{2}\)
Solution: Area of the label means the lateral area of the cylinder -> Just the area of the centre portion -> 2πrh
Substituting values, we get the answer to be 15 π/\(in^{2}\). The answer is D.
6. Spheres
SPHERES can be described as the three-dimensional equivalent of a circle. They have perfect symmetry, which means that all lines drawn from the center of the sphere to any point on the edge possess an equal length.
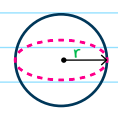
\(Volume=\frac{4}{3}\pi r^{3}\)
Surface Area = 4πr\(^{2}\)
Solved Example 7
Jenny gave Melissa a basketball for her birthday and she wrapped it in decorative paper. If the basketball has a diameter of 12 inches how much paper does Jenny use?
A. 112π /(in^{2}\)
B. 124π /(in^{2}\)
C. 144π /(in^{2}\)
D. 160π /(in^{2}\)
Solution: A basketball is a sphere, and when wrapping the outside of the sphere, you’re calculating the surface area.
\(Surface\: Area=4\pi r^{2}=4\pi 6^{2}=144\pi\)
C is the correct answer.
Inscribed Objects
Many standardized tests including the SAT will gauge your knowledge of three dimensional objects by increasing the complexity of questions. INSCRIBED OBJECTS is one way to add complexity to such a question. The most common combinations of inscribed objects include spheres in cubes, cubes in spheres, pyramids in spheres, prisms in cylinders, and cylinders in prisms.
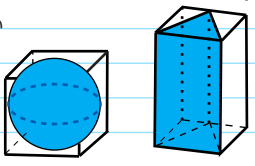
Solved Example 8
Suppose there is a sphere inscribed in a cube-like the one shown above on the left. The cube has a side length of 8 cm. If the sphere is filled completely with water, what is the volume of the cube that is not filled with water?
A. 243.93 /(cm^{3}\)
B. 252.54 /(cm^{3}\)
C. 264.25 /(cm^{3}\)
D. 270.42 /(cm^{3}\)
Solution: You're being asked to calculate the volume of a sphere and cube.
\(V_{cube}=S^{3}=8^{3}=512\)
\(V_{sphere}=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi 4^{3}=85.33\pi\)
Take the difference between the cube’s volume and the sphere’s volume to find your answer: \(V_{cube}-V_{sphere}=512-85.33\pi =249.93\: cm^{3}\)
The correct answer is A.
Diagonals of a Cube and Cuboid
The diagonal of a rectangular solid is the longest interior line of the solid. It touches from the corner of one side of the prism to the opposite corner on the other.
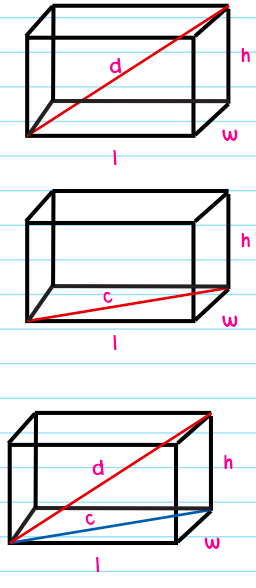
- You can find this diagonal by breaking up the figure into two flat triangles and using the Pythagorean Theorem for both.
- First, find the length of the diagonal (hypotenuse) of the base of the solid using the Pythagorean Theorem
\(c^{2}=l^{2}+w^{2}\) - Next, use that length as one of the smaller sides of a new triangle with the diagonal of the rectangular solid as the new hypotenuse:
\(d^{2}=c^{2}+h^{2}\)
The formulae is \(Diagonal\: of\: a\: Cuboid=\sqrt{(Length^{2}+Width^{2}+Height^{2})}\)
Cross-Sections
On the SAT, at times you’ll be asked about removing a slice or a cross-section from a 3D figure. Students often lose it when they see such a question on the test and rarely even attempt to solve it. However, these kinds of questions are pretty straightforward once you realize how cross-sections work.
If we slice a few 3D figures open with a plane, what are the possible cross-sections we’re left with?
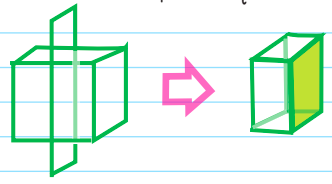
- If we cut a cube like below, we end up with a square (the shaded Z-D shape).
- If we cut a cube in a diagonal direction like below, we end up with a rectangle (as the shaded 2-D shape).
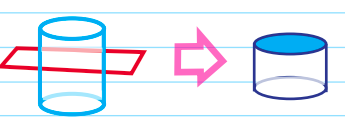
- If we slice a cylinder horizontally, the resulting Z-D cross section is a circle (the shaded region).
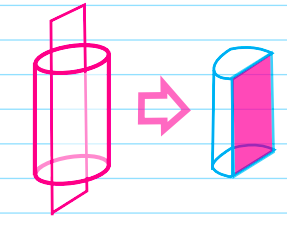
- If we slice a cylinder vertically, theresulting 2-D cross section is a rectangle (the shaded region).