Linear equations are equations in which all variables have an exponent of 1 and whose graph is a line.

A linear equation has the form: y = mx + b

Y represents every y-value on the line, m represents the slope (the ratio of RISE/RUN), and b represents the y-intercept (where a line crosses the y-axis). If you know the y-intercept, you know the value of y at the point where the line crosses the y-axis, and therefore, you also know the x-value there because it is always 0! If you know both the y-intercept and the slope of a line, you can graph the line.

But why stop at one line? We can take two linear equations and study them together, such as:

ax + by = c
dx + ey = f

This is known as SIMULTANEOUS LINEAR EQUATIONS. Because each of the linear questions represents a line, we can ask, “If I draw two lines, where do they intersect?” The process of finding the answer is called solving simultaneous equations.

There are three ways of doing it.

1. Graphing

We can solve simultaneous equations by GRAPHING each linear question and then finding where the lines intersect.

Example: Graph the simultaneous equations to find the solution.

x + y = 5
2x - y = 4

First rewrite each of the equations into the y = mx + b form to better graph each equation.

First equation: y = -x + 5
Second equation: y = 2x -4.

Then, graph the equations by siding the y intercept and slope from each.

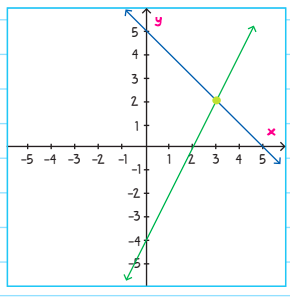
From the graph, we can see that the two lines intersect at (3, 2) - that is the solution of the simultaneous equations..

Example: Graph the simultaneous equations to find the solution.

2x + y = -2
2x + y = 3

In order to graph these more easily, change the first equation from 2x + y = -2 to y = -2x -2, and change the second equation from 2x + y = 3 to y = -2x + 3.

Then, we graph the two equations.

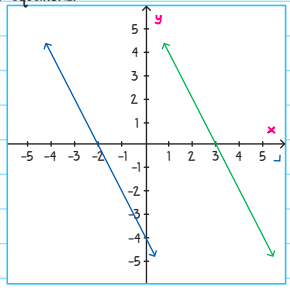
There are no intersection points, so there is no solution to the simultaneous equations. How can there by no solution? Let's look back at the original two learn equations:

1. The first linear equation is 2X + Y = -2
2. The second learn equation is 2X + Y = 3.

In other words, the equations tell us that 2X + Y will equal to -2 & 3 at the same time. Of course, this logically does not make sense because one expression cannot be equal to two different numbers at the same time. That is why there is no solution to these simultaneous equations.

Example: Graph the simultaneous equations to find the solution.

4x - 2y = 6
2x - y = 3

We can change the first equation from 4x - 2y = 6 to y = 2x - 3, and change the second equation from 2x - y = 3 to y = 2x - 3.

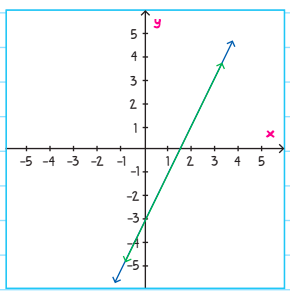
Graphing the two equations, we realize that they are the exact same line! In this case, we can see that the two lines overlap each other and intersect at every point along the line, so there are an infinite number of solutions to the simultaneous equations.

2. Substitution Method

We can also use algebra to solve simultaneous linear equations - one way is known as the substitution method. In the SUBSTITUTION METHOD, we find the solution by rewriting one equation and then substituting it into the other equation. This is the method we at AP Guru recommend our students use.

Example: Solve the simultaneous equations by using the substitution method.

4x + y = 7
3x + 2y = 9

First, rewrite equation as y = -4x + 7
and substitute it into equation : 3x + 2(-4x + 7) = 9

Now, we can solve for x: 3x - 8x + 14 = 9
-5x = -5
x = 1

Substituting x = 1 into either or , we find that y = 3,

So, the solution is (X, Y) = (1, 3).

3. Addition Method

The third way to solve simultaneous equations is by using ADDITION METHOD. The goal of the addition method is to eliminate either the x or y variable by adding their opposite. First, we multiply all the terms of one equation by a constant that will get one of the variables to add up to zero. Next, add the two equations together, to eliminate a variable, and then solve the simultaneous equations.

We can multiply the terms of both equations if that is what is necessary to solve the problem. Just find the least common multiple of the X’s or the Y’s and multiply each term accordingly to eliminate the variable.

Example: Solve the simultaneous equations by using the addition method.

4x - y = -7
-3x + 2y = 9

First, number the equations.

4x - y = -7
-3x + 2y = 9

Then multiply each term, in equation by 2 and call it equation 1:

8x-2y = -14

Now add equation and equation together:

8x - 2y = -14
-3x + 2y = 9

8x + (-3x) + (-2y) + 2y = -14 + 9

5x = -5
x = -1
Substitute x = -1 into either equation, we find that y = 3,

A GOOD TRICK

On the ACT math section, you’ll see countless problems that ask things like:

1. What is the value of X + Y?
2. What is the value of A - B?
3. What is the average of Z, X, and Y?
4. How much money did Ben and Chris raise together?
5. How many babies did the mother rabbit and the mother lion have in total?

In all of the above examples, it’s very tempting to find the values of X, Y, A, B, Z, Ben, and so on, but it’s also the worst imaginable strategy.

Before you solve for the value of any one variable, see if you’ll have an easier time finding the value of both. Some of the time, it won’t even be possible to find a single individual value.

For example, on a question like this: Two separate triangles have interior angle values of x, z, 17, d, 45, and 60, what is the value of x + z + d?

You can’t possibly figure out what x, z, or d equal independently. All you know is that both triangles combined have interior angle values of 180 + 180 = 360. So if you subtract 17, 45, and 60 from 360, you’ll have your answer.

Other problems could be solved by substitution and/or hard math, but simply figuring out what everything equals together solves them much more easily.

Example: What’s the value of A + B + C if
3A + 6B + 19C = 12,
A + 2B + 7C = 9,
and 25A + 21B + 3C = 8?

At first, that problem seems like a total nightmare...until you stack them up and simplify everything

3A + 6B + 19C = 12
A + 2B + 7C = 9
25A + 21B + 3C = 8
29A + 29B + 29C = 29
=> A + B + C = 1

We have literally no idea what A, B, or C equal - and we shouldn't care.

Once you start looking for ways to use this strategy, you’ll realize that it’s useful all the time. Yes - there are a few problems here and there that actually force you to find the values of each independent variable, but they are rare.