Lines and Angles

There are only a couple of Lines and Angles questions tested on the ACT Math section. The questions are usually easy and should not pose a challenge to you.

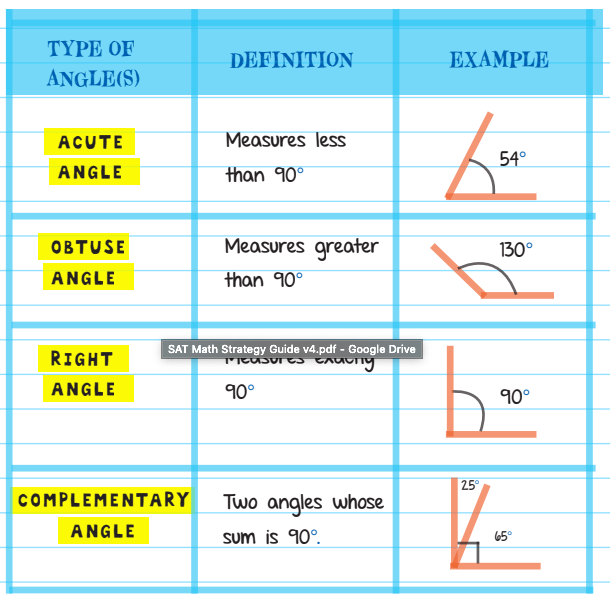
Here's a quick breakdown of the different types of angles:

Transversal Lines

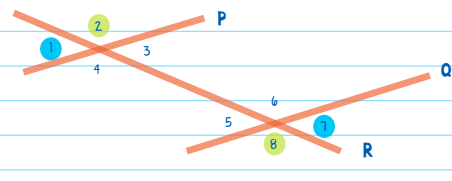
A transversal line is a line that cuts through two parallel lines. A transversal line creates eight angles. But by studying the angles, we can see that many of the angles are congruent! In the diagram below, line R is a transversal line that cuts through lines P and Q, which are parallel to each other.

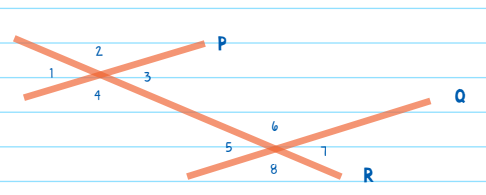
A transversal line creates eight angles. But by studying the angles, we can see that many of the angles are congruent! We know that ∠1 is congruent to ∠3 because they are vertical angles. For the same reason, we know that the following angles are also congruent:

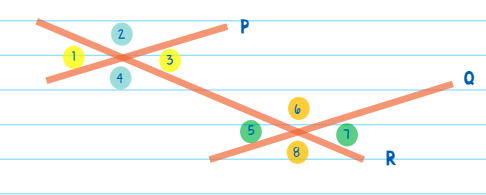
∠2 = ∠4
∠5 = ∠7
∠6 = ∠8

But what else do we know? Because P and Q are parallel, the transversal forms CORRESPONDING ANGLES - angles that are in the same position in relation to the transversal and therefore congruent. Thus, the following corresponding angles are congruent:

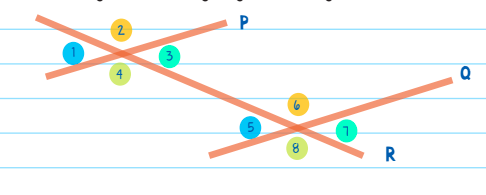
∠1 = ∠5
∠2 = ∠6
∠3 = ∠7
∠4 = ∠8

Furthermore, because P and Q are parallel and cut by the transversal, it means that ∠1 is congruent to ∠7 because they are ALTERNATE EXTERIOR ANGLES. Alternate exterior angles are on opposite sides of a transversal and outside the parallel line. Thus, the following alternate exterior angles are congruent:

∠1 = ∠7
∠2 = ∠8

Similarly, because P and Q are parallel, it means that ∠3 is congruent to ∠5 because they are ALTERNATE INTERIOR ANGLES - angles that are on opposite sides of a transversal and inside the parallel line. For the same reason, ∠4 is congruent to ∠6.

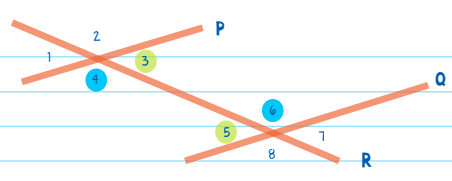
∠4 = ∠6
∠3 = ∠5

So, putting all information together:
∠1, 3, 5 and 7 are congruent;
∠2, 4, 6 and 8 are congruent.

The opposite of all of this is also true: if you don't know if two lines are parallel - look at the alternate interior or exterior angles. If they are congruent, the lines are parallel.

Solved Example 1 
Statement A: ∠3 + ∠4 + ∠5 = 131°
Statement B: ∠6 + ∠7 + ∠8 = 131°

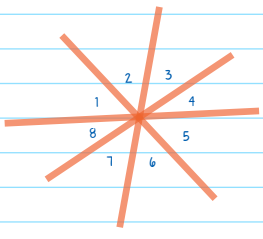
Refer to the figure and two statements. Evaluate ∠1 + ∠2.
A. 82°
B. 98°
C. 180°
D. 262°

Solution: Let’s consider the first statement by itself. ∠2, ∠3, ∠4, and ∠5 together form a straight angle, so their degree measures a total 180°.

∠2 + ∠3 + ∠4 + ∠5 = 180°
∠2 + 131° = 180°
∠2 = 49°

Without further information, no other angle measures, including that of ∠1, can be found. So, let’s consider the second statement. ∠1, ∠6, ∠7, and ∠8 together form a straight angle, so their degree measures a total 180°.

∠1 + ∠6 + ∠7 + ∠8 = 180°
∠1 + 131° = 180°
∠1 = 49°

We’ve found both ∠1 and ∠2, so all we have to do is add them together to solve the problem:

∠1+ ∠2 = 49° + 49° = 98°

The correct answer is B.

Solved Example 2 
Statement A: ∠2 = 89°
Statement B: ∠3 = ∠6

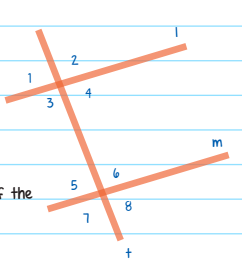
Given the above figure and two statements, which of the following is true?
A. Line m is perpendicular to line t
B. Line m is not perpendicular to line t
C. ∠4 = ∠7
D. ∠1 = ∠6

Solution: Statement A alone establishes by definition that line l is not perpendicular to line t, but it does not establish any relationship between line m and line t.

By Statement B alone, we know line l is parallel to line m because alternating interior angles are congruent., line l is parallel to line m. ∠2 and ∠6 are corresponding angles formed by a transversal across parallel lines, so ∠6 = ∠2 = 89°. ∠6 is not a right angle, so line m is not perpendicular to line t and B is the correct answer.

Solved Example 3

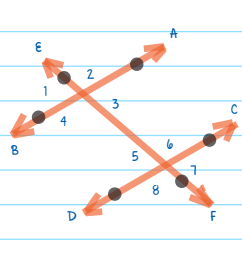
Consider the line diagram shown at right. Which of the following pieces of information is enough to prove that AB is parallel to CD?
A. ∠1 = ∠3
B. ∠4 = 120° and ∠8 = 60°
C. ∠5 = 120° and ∠6 = 60v
D. ∠2 = ∠6 = 100°

Solution: By learning that ∠4 = 120° and ∠8 = 60°, we have enough information to determine that ∠1 = 60° (because it forms a straight angle with ∠4 ) and that ∠7 = 120° (since it forms a straight angle with ∠8 ). At this point, we can see that the pairs of corresponding angles, angles 1 and 8 and angles 4 and 7, match in value. This means that AB is parallel to CD. The correct answer choice is B.

Solved Example 4

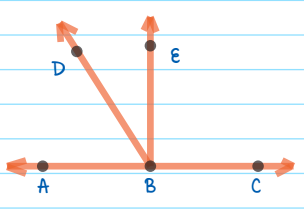
∠ABD = 60°. What is ∠DBE?
A. 30°
B. 45°
C. 60°
D. 90°

Solution: The sum of ∠ABD, ∠DBE, and ∠EBC equally 180° because they are all on the straight-line AC.
∠ABD + ∠DBE + ∠EBC = 180°

We know that ∠ABD = 60° and that ∠EBC = 90°, so we can substitute in those values.
60° + ∠DBE + 90° = 180°
∠DBE = 30°‍

The correct answer is A.

Standard Position of Angles

An angle is said to be in standard position if its vertex is positioned at origin and one line is at the positive -axis. The line on the -axis is called the initial side, and the other line is called the terminal side.

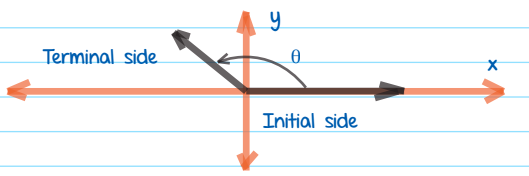
The rotation from the initial side to the terminal side is a measure of an angle. The counterclockwise rotation is considered positive. An angle in the clockwise direction is taken as negative. CO-TERMINAL angles are the two angles that have the same terminal side.

Radians and Degrees

RADIANS and DEGREES are units to measure angles. The conversion between these two units can be done using the following equation.

\(\frac{1}{360} degree=\frac{1}{2\pi}radian\) OR
\(\frac{1}{180} degree=\frac{1}{\pi}radian\)‍

To convert from degrees to radians and vice versa, we need the following:
Deg. = Rad. x \(\frac{180}{\pi}\)
Rad. = Deg. x \(\frac{\pi}{180}\)

For example, if we need to convert 50 degrees to radians, we need to multiply the degree measure by \(\frac{\pi}{180}\) ,

i.e. 50°= 50 x \(\frac{\pi}{180}rad = \frac{5\pi}{18}rad\)

Similarly, if we need to convert radians into degrees, we need to multiply the radian measure by \(\frac{\pi}{180}\)

Some important conversions are:

• \(30^{\circ}=\frac{\pi}{6}rad.\)
• \(45^{\circ}=\frac{\pi}{4}rad.\)
• \(60^{\circ}=\frac{\pi}{3}rad.\)
• \(90^{\circ}=\frac{\pi}{2}rad.\)
• \(180^{\circ}=\pi rad.\)

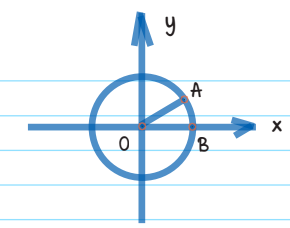
Example: In the xy-plane, O is the center of the circle, and the measure of radians. What is the value of a?

By the distance formula, the length of radius OA is \(\sqrt{\sqrt{3^{2}}+1^{2}}=2\)

Thus, SIN (∠AOB) = \(\frac{1}{2}\)

Therefore ∠AOB is 30°, which is equal to \(30\frac{(\pi)}{180}=\frac{\pi}{6}radians\)

Hence, the value of a is 6.