Co-ordinate Geometry
COORDINATE GEOMETRY is the study of geometry on a plane using a coordinate system. This plane is called a COORDINATE PLANE, which has scales of measurement along the x and y-axes.
Slope of a Line
SLOPE is a number that is a ratio that describes the tilt of a line:
\(SLOPE=\frac{RISE}{RUN}\)
RISE is how much a line goes up or down.
RUN is how much a line moves left or right.
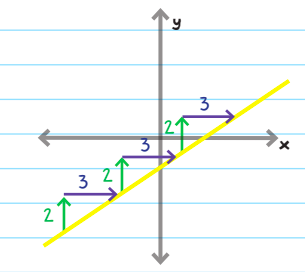
Example: A line with a slope of 2/3
Rise = 2
Run = 3
\(Slope=\frac{RISE}{RUN}\)
A slope of 2/3 means that every time the line rises 2, it also runs 3.
To find the slope of the line, pick any two points on the line. Starting at the point farthest to the left, draw a right triangle that connects the two points and uses the line as the hypotenuse.
How many units did you go up or down? That is your rise. How many units did you go left or right? That is your run. Put your rise over your run, and you have the slope.
Example: Find the slope of the line.
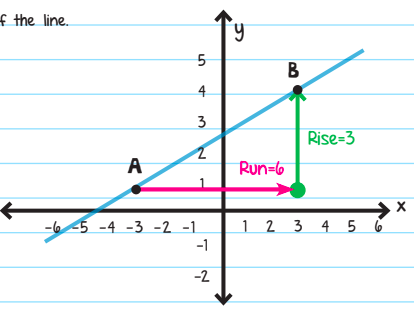
Rise = 3
Run = 6
\(Slope=\frac{3}{6}=\frac{1}{2}\)
There is also a FORMULA FOR SLOPE that you can use when you know two points on a line: \(Slope=\frac{the\: change\: in\: y}{the\: change\: in\: x}\: or\: m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Example: Find the slope of the line that goes through (Z, 3) and (4, 6).
Label each given value as \((x_{1},y_{1})and(x_{2},y_{2})\)
\(x_{1}=2,y_{1}=3,x_{2}=4,y_{2}=6\)
Use the slope formula and substitute the values:
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{6-3}{4-2}=\frac{3}{2}\)
\(Slope=\frac{3}{2}\)
You can also graph a line if you know only one point and the slope. You have all the information you need - a starting point, the number of units it rises, and the number of units it runs.
Please Note:
- The slopes of two parallel lines are always equal.
- The product of the slopes of two perpendicular lines is -1, for instance, \(m_{1}\) x \(m_{2}=-1\)
Solved Example 1
In the xy coordinate plane, how many points are a distance of 4 units from the origin?
A. Two
B. Three
C. Four
D. More than four
Solution: For a question like this, it may be tempting to answer D, four. After all, there will be four distinct points 4 units from the origin, two on the x-axis (one right and one left), and two on the y-axis (one up and one down).
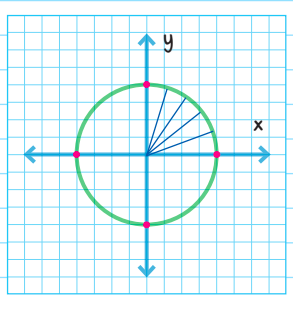
But answering this way would disregard the realities of circles. Imagine that we have a circle with a midpoint at the origin whose circumference touches each of the points 4 units from the origin. Now, if we remember our circle definitions, we know that all straight lines drawn from the center of the circle to the circumference will all be equal.
This means that there will be infinitely many points that are 4 units from the origin. These points may have “weird” coordinates (as in non-integer values), but they will be points 4 units from the origin all the same. The correct answer is D, more than four.
Solved Example 2
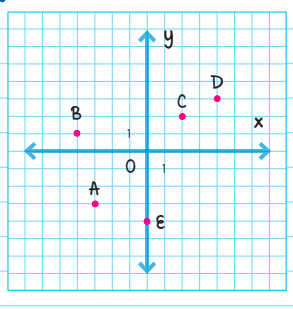
Which of the lettered points in the figure below has coordinates (x, y), such that |x| + |y| = 5
A. A
B. B
C. C
D. D
Solution: For a question like this, the most efficient path is to work from our answer choices. Point A is at coordinates (-3, -3). So let's find the sum of their absolute values.
|x| + |y| = |−3| + |−3| = 3 + 3 = 6
Since we are looking for the value 5, this answer is too large.
Point B is at coordinates (-4, 1) = |x| + |y| = |−4| + |1| = 5
Success! We have found the answer choice that gives us coordinates whose absolute values add up to 5. Because there will only ever be one correct answer on any SAT question, we can stop here. The correct answer is B.
Types of Slopes
There are four types of slope:
- Positive Slope- rises from left to right
- Negative Slope- falls from left to right
- Zero Slope - is horizontal because the rise is 0, and 0 divided by any number is 0
- Undefinied Slope - is a vertical line because the run is 0, and any number divided by 0 is undefined
Intercept of a Line
An intercept of a line is a point where a line meets the coordinate axis. There are two types of intercepts.
- x-intercept - point on the line at which y = 0.
- y-intercept - the y-intercept is the point on the line at which x = 0.
In the diagram, the x-intercept is -4, as expressed by the ordered pair (-4, 0). The y-intercept is 6, as expressed by the ordered pair (0, 6).
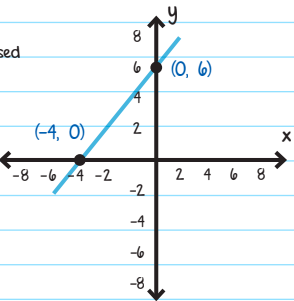
To find x-intercepts, plug in 0 for y.
To find the y-intercepts, plug in 0 for x.
Solved Example 3
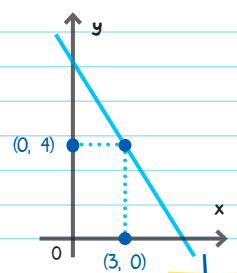
In the above figure, if line l, has a slope of -2, what is the y-intercept of l ?
A. 7
B. 8
C. 9
D. 10
Solution: We can see that the rectangle has a length of 3 and a height of 4. This means that the rectangle hits the line at the top right corner at coordinates (3, 4). Therefore, Point (3, 4) lies on the line. Additionally, the slope of the line is given as -2. Let's plug in the value of the slope in the equation of a line formulae
y = mx + c (more on this later)
Y = -2x + c.
To find the value of c, plug in the values of the point (x, y) -> (3, 4)
4 = -2 (3) + c
c = 10
This is also our y-intercept. The correct answer is D.
Equation of a Line
All lines can be expressed in an equation form. The most general form of equation for a line is where m is the slope of a line and c is a y-intercept of a line.
y = mx + c .....slope-intercept form
If you are given the two points, you can easily find the equation of a line.
Example: Points, P (2, -3) and Q (-4, 1), lies on the line, l. First you need to find the slope of a line:
\(M=-\frac{2}{3}\)
Substitute in the equation above: \(y=-\frac{2}{3}x+c\)
Now we can use either of the points to find c. Note that both points will give the same value of c. Let’s use P (2, -3): \(-3=-\frac{2}{3}(2)+c\)
\(c=-\frac{5}{3}\)
Therefore, the equation of the line l is: \(y=-\frac{2}{3}x-\frac{5}{3}\)
or can be written as 3y + 2x = -5
Horizontal and Vertical Lines
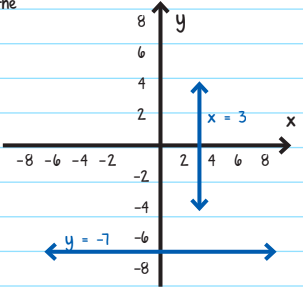
Horizontal and vertical lines are not expressed in the y = mx + b form.
Horizontal lines are expressed in the form: y = constant
In the above example, y = -7.
Vertical lines are expressed in the form: x = constant
In the above example, its x = 3.
Midpoint Formula
If you have been given two coordinate points, you can use a formula to find the midpoint of the two points. The midpoint of the two points \(P(x_{1},y_{1})\: and\: Q(x_{2},y_{2})\) is given by \(M=(\frac{x_{1}-x_{2}}{2}),(\frac{y_{1}-y_{2}}{2})\)
For example, if we have two points P (2, -3) and Q (-4, 1), then the distance is \(M=(\frac{2-4}{2}),(\frac{-3+1}{2})\)
Distance Formula
\(d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)
The subscripts just show that there is a first point and a second point - it does not matter which point you call first or second.
Point D is located at (11, -2). Point E is located at (7,-5). What is the distance between D and E?
First, assign the first and second coordinates values: \(x_{1}=11,\: y_{1}=-2,\: x_{2}=7,\: y_{2}=-5\)
Then, plug the values into the formula:
\(d=\sqrt{(7-11)^{2}+(-5-2)^{2}}\)
\(d=\sqrt{(-4)^{2}+(-3)^{2}}\)
\(d=\sqrt{16+9}\)
d=5
Therefore, Points D and E are 5 units apart.
Solved Example 4
Rosa and Marco met up for dinner and then drove home separately from the restaurant. To get home from the restaurant, Rosa drove north 6 miles and Marco drove west 8 miles. How far apart do Rosa and Marco live?
A. 6 miles
B. 8 miles
C. 10 miles
D. 12 miles
Solution: Let us make a quick sketch of our scenario.
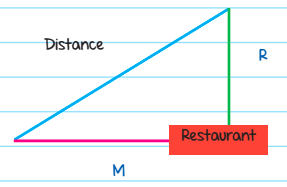
Rosa drove 6 miles north and Marco drove 8 miles west, which means that the legs of our triangle will be 6 and 8. Now we can find the hypotenuse by using the Pythagorean Theorem.
\(c^{2}=6^{2}+8^{2}\)
\(c^{2}=100\)
c = 10
The correct answer is C, 10 miles.