
Miscellaneous Algebra
There are a few additional algebra topics often tested on the SAT. Expect each of the following to show up at least once on each SAT Math Test.
1. Undefined Denominator
Math convention does not allow division by 0. When 0 appears in the denominator of an expression, then that expression is undefined. How does this convention affect quadratic equations?
Example: What are the solutions to the following equation?
\(\frac{x^{2} + x - 12}{x - 2} = 0\)
We notice a quadratic equation in the numerator. Since it is a good idea to start solving quadratic equations by factoring, we will factor this numerator as follows: \(\frac{(x-3)(x-4)}{x-2} = 0\)
If either of the factors in the numerator is 0, then the entire expression becomes 0. Thus, the solutions to this equation are x = 3 or x = - 4.
Rationalizing of Denominator
The SAT generally does not include in its answer choices any mathematical expressions in which a radical ( \(\sqrt{}\) ) appears in the denominator of a fraction. Accordingly, if your calculations yield a radical in the denominator, you should be prepared to take one last step: rationalize the denominator.
\(\frac{3}{\sqrt{2}}\rightarrow Multiply\: by \frac{\sqrt{2}}{\sqrt{2}}\: To \: get \: \frac{3\sqrt{2}}{2}\)
If the radical includes two terms, either added or subtracted, your job becomes significantly more difficult. Fortunately, there’s a method that can help you.
Example: What is the value of \(\frac{2}{2-\sqrt{2}}\)
In this problem, the multi-part denominator poses an algebraic challenge. Try to multiply both the numerator and denominator by the denominator, and you are still left with a messy radical in the denominator. Algebraically, the solution is to employ the difference of squares:
\(\frac{2}{2-\sqrt{2}}\) x \(\frac{2+\sqrt{2}}{2+\sqrt{2}}\)
\(\frac{4 + 2\sqrt{2}}{2^{2}-\sqrt{2^{2}}}\)
\(\frac{4+2\sqrt{2}}{2}\)
\(2+\sqrt{2}\)
When rationalizing denominators with addition or subtraction in them, the difference of squares rule is a nearly magical way to transform the expression.
2. Direct and Inverse Proportions
Direct Variation: As one value increases, the other value increases. Decreases in one variable produce a decrease in the other.
Example:
- 10 doughnuts cost $6.00. How much will 15 doughnuts cost?
- Set up proportion 6/10 = x/15
- x = $9.00 or use 6/10 as the constant of variation.
- The constant stays the same no matter what amount is purchased.
- If you want 15, then $0.6x15 = $9.00
- If you want 45, then $0.6 x 45 = $27.00
Inverse Variation: A change in one variable produces an inverse or opposite change in the other.
Solved Example 1
Travelling at a constant rate of 50 mph, a trip takes 2 hours. How long (in minutes) will the trip take if you travel at 60 mph?
A. 90
B. 100
C. 110
D. 120
Solution: You should recognize right away that this is an inverse. As the rate of travel increases, the time decreases. One way to solve for the correct answer is to find the constant of variation → the distance. Once you find distance, you can solve for time.
D = 50 mph x 2 hours = 100
100 = 60 mph x t
100/60 = t = 1 2/3 hours = 1 hour 40 mins.
The correct answer is B.
3. Exponential Growth and Decay
SAT Math Test problems can deal with the growth or decline of populations of bacteria or other organisms. They are modeled on the following equations:
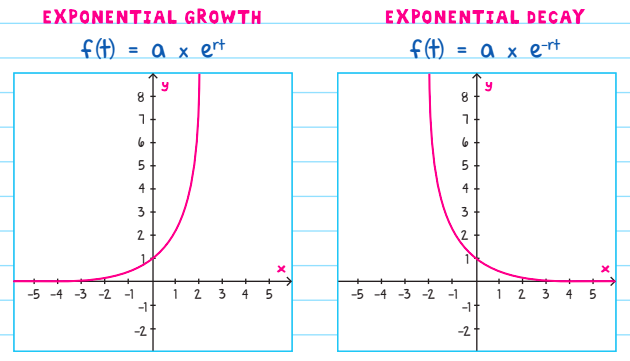
a = Constant specified in problem
e = Numerical constant ≈ 2.718
r = Rate of growth/decay
t = Time
The key difference between growth and decay is that growth has an exponential increase, while decay has an exponential decrease.
Solved Example 2
A scientist places an initial population of 3.5 x \(10^{4}\) bacteria on a plate containing glucose. She knows that this type of bacteria, when supplied with abundant glucose, can double every 2 hours. When she checks on the bacteria at the same time the next day, approximately how many bacteria should she expect to find, assuming the bacteria do not run out of glucose to eat?
A. 9.27 x \(10^{12}\)
B. 9.27 x \(10^{14}\)
C. 9.35 x \(10^{14}\)
D. 9.35 x \(10^{16}\)
SOLUTION: This is an exponential growth question, so we need to start with the correct formula.
f(t) = a x \(e^{rt}\)
Next, we should organize the information we’re given:
a = 3.5 x \(10^{4}\) (Initial population)
t = 12 (The scientist checks on the bacteria at “the same time the next day,” so 24 hours have passed. The rate of this problem is given as applying every 2 hours, though, so we have 12 2-hour periods’ worth of bacteria growth to account for).
r = 2 (Population is said to “double” every 2 hours).
We’re solving for the number of bacteria after 24 hours have passed - in mathematical terms, f(t). Plugging the given information into the exponential growth formula, we can solve for the unknown variable.
f(t) = 3.5 x \(10^{4}\) x \(e^{2 x 12}\)
f(t) = 3.5 x \(10^{4}\) x \(e^{24}\)
f(t) = 9.27 x \(10^{14}\)
The correct answer is B
Solved Example 3
A special lizard population is in danger of becoming extinct. In 1920, the blue speckled lizard population contained 3.78 x \(10^{7}\) individuals. It has decreased by 2% every year since. If the rate of decay continues in this fashion, in what year will the population be roughly 6.25 x \(10^{6}\) ?
A. 2008
B. 2010
C. 2012
D. 2014
SOLUTION: Identify all known information
1. Initial year = 1920
2. Initial population (a) = 3.78 x \(10^{7}\)
3. Decaying exponential problem (R) - “decreasing by 2%” represents the rate of decay
4. Final population f(t) = 6.25 x \(10^{6}\)
In mathematical terms we have: \(P=ae^{-rt}\)
6.25 x \(10^{6}\) = 3.78 x \(10^{7}e^{-0.02t}\)
Divide by 3.78 x 10.
0.165 = \(e^{-0.02t}\)
Take the natural log of both sides. (The natural log and e cancel each other out).
ln (0.165) = ln \((e^{-0.02t})\)
ln (0.165) = -0.02t
t = 90
From here, to find the year, we will need to add t to the initial year.
Y = t + 1920
= 2010
B is the correct answer!
Solved Example 4
Tina works at a university where the student population has seen growth over the last 50 years. In 1950 the student population was 500, and on average, every year it increases by 4%. If the university continued to grow in this way, how many students were in the class of 2015?
A. 6732
B. 6744
C. 6740
D. 6791
Solution:
1. “Growth” represents an exponential growth problem.
2. “In 1950, the student population was 500” gives the starting time and population.
3. “Every year” represents our time unit. We will need to calculate the specific time by sub- tracting the initial time from the time in question: 2015 − 1950 = 65
4. “Increases by 4%” represents the rate.
In mathematical terms, we have:
\(P=ae^{rt}\)
\(P=500e^{0.04\; x\; 65}\)
P = 500e2.6
P = 6732
The correct answer is A.
Rates and Work
One common type of word problem on the SAT Math Test is the rate problem. Rate problems come in a variety of forms, but all are marked by three primary components: rate, time, and distance/work.
These three elements are related by the following equations:
- RATE X TIME = DISTANCE (RT = D)
- RATE X TIME = WORK (RT = W)
The SAT makes rate situations more complicated by involving more than one person or vehicle traveling. To deal with this, you will need to consider multiple RT = D relationships.
Example: Harvey runs a 30-mile course at a constant rate of 4 miles per hour. If Clyde runsthe same track at a constant rate and completes the course in 90 fewer minutes, how fast did Clyde run?
Both Harvey and Clyde ran the same course, so the distance they both ran was 30 miles. Additionally, you know Clyde ran for 90 fewer minutes. If Harvey ran t hours, then Clyde ran (t - 1.5) hours:

Now you can solve for t:
4t = 30
t - 7.5
If t= 7.5, then Harvey ran for 7.5 - 1.5 = 6 hours. You can now solve for Harvey’s rate. Let r equal Harveys rate:
r x 6 = 30
r = 5
4. Relative Rates
Relative rate problems are a subset of multiple rate problems. The defining aspect of these problems is that two bodies are traveling at the same time. There are three possible scenarios:
- The bodies move towards each other.
- The bodies move away from each other.
- The bodies move in the same direction on the same path.
Solved Example 5
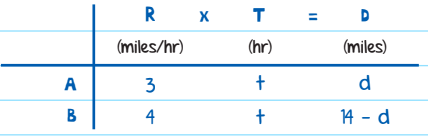
Imagine that two people are 14 miles apart and begin walking towards each other. Person A walks 3 miles per hour, and Person B walks 4 miles per hour. How long will it take them to reach each other?
A. 1
B. 2
C. 3
D. 4
Solution: The time that each person walks is exactly the same (t hours), and the total distance they walk is 14 miles. If one person walks d miles, the other walks (14 - d) miles. The chart would look like this:
The rate at which they’re getting closer to each other is 3 + 4 = 7 miles per hour. In other words, after every hour they walk, they are 7 miles closer to each other. Now you can create one RT = D equation:
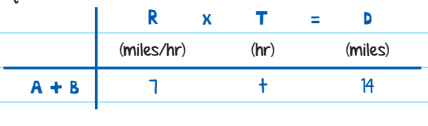
7t = 14
t = 2
The correct answer is B. You may very well have answered this question intuitively. But as the questions become more difficult, this method only becomes more valuable.
Solved Example 6
Car X is 40 miles west of Car Y. Both cars are traveling east, and Car X is going 50% faster than Car Y. If both cars travel at a constant rate and it takes Car X 2 hours and 40 minutes to catch up to Car Y, how fast is Car Y going?
A. 20 miles per hour
B. 30 miles per hour
C. 40 miles per hour
D. 50 miles per hour
Solution: The multiple RTD chart would look like this:
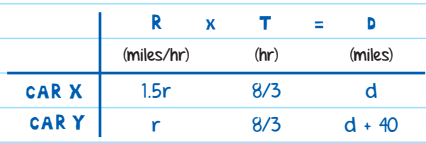
Instead, you can answer this question with one equation. If Car X is initially 40 miles behind Car Y, and they both travel until Car X catches up to Car Y, then the distance between them will have decreased by 40 miles. That is your distance. The distance between the two cars is decreasing at a rate of 1.5r - r = 0.5r, and the time they travel is 8/3 hours:
0.5r x 8/3 = 40
r = 30
You defined the rate Car Y was traveling as r, so if r = 30, then Car Y was going 30 miles per hour. The correct answer is B.
5. Work Problems
Work problems are just another type of rate problem. Instead of distances, however, these questions are concerned with the amount of work done.
Work takes the place of distance. Instead of RT = D, use the equation RT = W.
Be sure to express a rate as work per time (W/T), NOT time per work (T/W).
For example: if a machine produces pencils at a constant rate of 120 pencils every 30 seconds, the rate at which the machine works is 120 pencils/30 seconds = 4 pencils/second.
Example 7
Martha can paint 3/7 of a room in 4.5 hours. If Martha finishes painting the room at the same rate, how long will it have taken Martha to paint the room?
A. 8.3 hours
B. 9 hours
C. 9.5 hours
D. 10.5 hours
SOLUTION: The first step in this problem is to calculate the rate at which Martha paints the room. You can say that painting the entire room is completing 1 unit of work. Set up an RTW chart:

Now you can solve for the rate:
r x \(\frac{9}{2}=\frac{3}{7}\)
r = 2/21
The division would be messy, so leave it as a fraction. Martha paints 2/21 of the room every hour. Now you have what you need to answer the question. Remember, painting the whole room is the same as doing 1 unit of work. Set up another RTW chart:

\(\frac{(21)}{2}t = 1\)
\(t=\frac{21}{2}\)
The correct answer is D. Notice that the rate and the time in this case were reciprocals of each other. This will always be true when the amount of work done is 1 unit.
6. Working Together
More often than not, work problems will involve more than one worker. When two or more workers are performing the same task, their rates can be added together.
For instance, if Machine A can make 5 boxes in an hour, and Machine B can make 12 boxes in an hour, then working together the two machines can make 5 + 12 = 17 boxes per hour.
Likewise, if Lucas can complete 1/3 of a task in an hour and Serena can complete 1/2 of that task in an hour, then working together they can complete 1/3 + 1/2 = 5/6 of the task every hour.
If, on the other hand, one worker is undoing the work of the other, subtract the rates. For instance, if one hose is filling a pool at a rate of 3 gallons per minute, and another hose is draining the pool at a rate of 1 gallon per minute, the pool is being filled at a rate of 3 - 1 = 2 gallons per minute.




