Polygons
The polygons tested on the SAT include the following:
- Three-sided shapes (Triangles)
- Four-sided shapes (Quadrilaterals)
- Other polygons with n sides (where n is five or more)
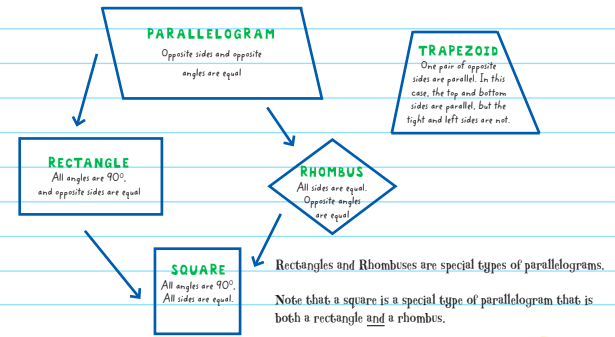
This chapter will focus on polygons of four or more sides. In particular, we will focus on the following four-sided polygons, or quadrilaterals: trapezoids, parallelograms, and special parallelograms, such as rhombuses, rectangles, and squares.
Quadrilaterals
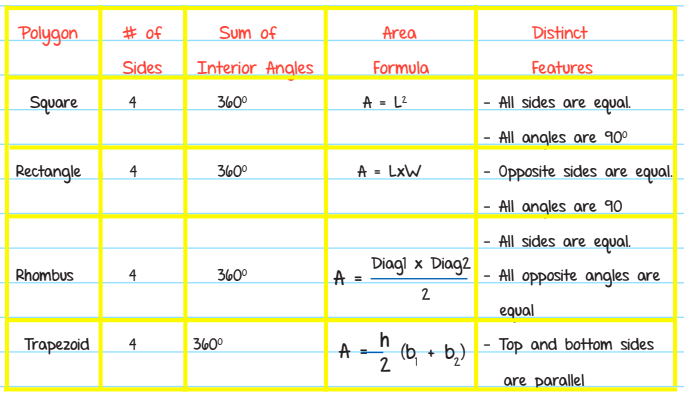
The most common polygon tested on the SAT, aside from the triangle, is the QUADRILATERAL (any four-sided polygon). Almost all SAT polygon problems involve the special types of quadrilaterals shown below.
Regular and Irregular Polygons
A regular polygon is one that has sides of equal lengths and equal angles. For example, equilateral triangles, squares, pentagons are regular polygons.
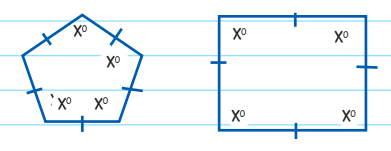
An irregular polygon is one that does not have equal sides or angles. The most basic example is a rectangle. Other irregular polygon examples are trapezoid, parallelogram, and kite shapes.
Area of a Polygon
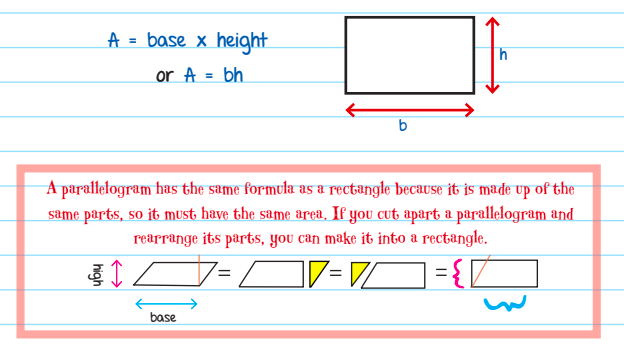
Most of the polygon-based questions on the SAT Math Test will demand you identify the area and the perimeter of a figure. In order to calculate the AREA OF A PARALLELOGRAM, multiply the base by the height. (This formula applies to rectangles, rhombuses, and squares, too.)
In order to calculate the AREA OF a TRAPEZOID, use the formula:
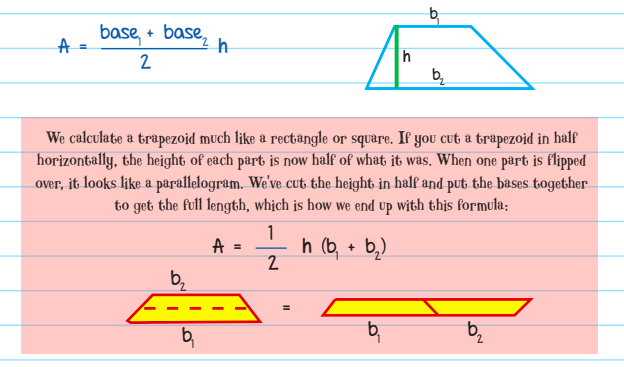
\(A=\frac{base_{1}+base_{2}}{2}h\)
Solved Example 1
In the figure, WXYZ is a rectangle with WA = BZ = 4. The area of the shaded region is 32. What is the length of XY?
A. 8
B. 10
C. 16
D. 20
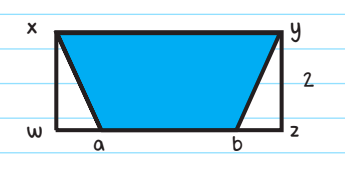
Solution: First, let us fill in the given information:
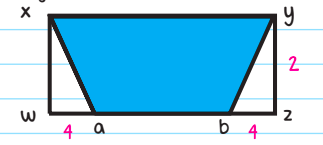
Now if we call the longest base q, the shortest base will be q−4−4, or q−8. (Why? Because the shortest leg is equal to the longest leg minus our two given lengths of 4).
\(Area_{trapezoid}=\frac{1}{2}h(b_{1}+b_{2})\)
\(32=\frac{1}{2}2\left ( q+q-8 \right )\)
32 = 2q - 8
20 = q
The length of XY (which we designated q) is 20. The correct answer is D.
Solved Example 2
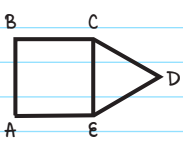
In the figure above, CDE is an equilateral triangle and ABCE is a square with an area of 1. What is the perimeter of polygon ABCDE?
A. 4
B. 5
C. 6
D. 7
Solution: We are told that ABCE is a square with the area of 1. This means that AB, BC, CE, and AE are ALL equal to 1. We also know that CED is an equilateral triangle, which means that each side length is equal. Since we know that CE = 1, we know that CD and DE both equal 1 as well.
So the perimeter of the polygon as a whole - which is made of lines AB, BC, CD, DE, and EA - is equal to: 1 + 1 + 1 + 1 + 1 = 5
The correct answer is B.
Area of Compound Polygons
The best way to find the area of a complex polygon is to split the polygon into smaller shapes, find the area of each small shape, and finally add those areas together.
Example: Find the area of the following compound shape.
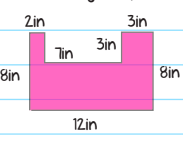
We first break it up into smaller quadrilaterals:
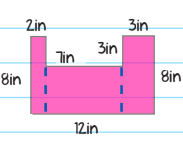
In other words, we have three smaller quadrilaterals that look like this:
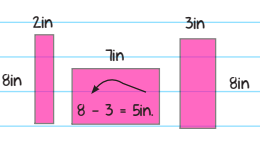
Calculating the area of each of the quadrilaterals and adding them all up looks like this:
Area = 2 x 8 + 7 x 5 + 3 x 8
A = 16 + 35 + 24
\(A=75\: in^{2}\)
Angles of a Polygon
The sum of the interior angles of a given polygon depends only on the number of sides in the polygon. The sum of the interior angles of a polygon follows a specific pattern that depends on n, the number of sides that the polygon has.
Sum of Interior Angles of a Polygon = (n - 2) x 180°
For example:
- A triangle has three sides, therefore, the sum of its angles is, S = (3-2) x 180°= 180°
- For a quadrilateral, S = (4-2) x 180°= 360°
- For a pentagon, S = (5-2) x 180°= 540°
- For a hexagon, S = (6-2) x 180°= 720°
To find the individual interior angle, θ, of a regular polygon, simply divide the sum of angles, S, by the number of sides, n, i.e. \(\Theta =\frac{n-2}{n}\) x 180°
Solved Example 3
A regular polygon with n sides has equal angles of 120°. How many sides does the figure have?
A. 4
B. 5
C. 6
D. 7
Solution: The formulae for angles of a polygon is: \(\Theta =\frac{n-2}{n}\) x 180°
Here, θ = 120°
\(120 =\frac{n-2}{n}\) x 180
n=6
The correct answer is C.
Solved Example 4
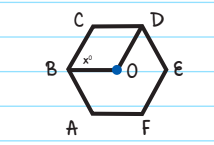
In the figure, ABCDEF is a regular hexagon, and its center is point O. What is the value of x?
A. 30
B. 40
C. 60
D. 80
Solution: Because this hexagon (n = 6) is regular, we can find the degree measure of each of its interior angles.
\(\Theta =\frac{n-2}{n}\) x 180°
\(\Theta =\frac{6-2}{6}\) x 180°
θ = 120°
Now the line BO is at the center of the figure, so it bisects the interior angle CBA. The angle CBA is 120°, which means that angle x will be 60°. The correct answer is C.
Solved Example 5
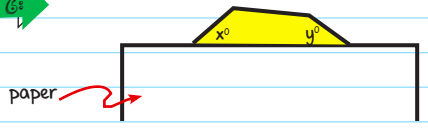
In the figure above, a shaded polygon that has equal sides and equal angles is partially covered with a sheet of blank paper. If x + y =80, how many sides does the polygon have?
A. 7
B. 8
C. 9
D. 10
Solution: We are told that the larger polygon has equal sides and equal angles. We can also see that the yellow coloured figure is a quadrilateral. We know that a quadrilateral is 360°, so let us subtract our givens from 360°
We have been given that X + Y = 80°.
Therefore, the remaining two angles = 360° − 80° = 280°
Again, we know that the polygon has all equal angles, so we can find each angle of the polygon by dividing by 2. Each angle of the polygon is 140°
\(140=\frac{(n-2)}{n}\\) x 180
14n = 18(n-2)
9 = n
The correct answer is C.
Diagonals of a Polygon
The diagonals of a polygon are the line segments from one vertex of the polygon to the other (non-adjacent) vertex. For an n-sided polygon, the number of diagonals (d) can be found using the following: \(d=\frac{n(n-3)}{2}\)
A decagon has \(d=\frac{10(10-3)}{2}=35\) diagonals
Note that triangles have no diagonals. Also note that the product n(n-3) is divided by two because each diagonal has two ends, so it would count each one twice.
The properties of some common polygons are summarized in the table below: