Trigonometry

The word TRIGONOMETRY is Greek; tri means three, gon means angle and meter means to measure. Combining all these three words, we get, “three angle measure”. The logic behind this is that trigonometry involves the measurements inside a triangle, which has three angles.

SOHCAHTOA

Trigonometry is based upon three primary relationships within a triangle. The mnemonic SOHCAHTOA has been commonly used to help students memorize the associations between the sine, cosine, and tangent in a right triangle. These trigonometric identities are used to find missing components of a right triangle.

SOH: Sine of θ equals the Opposite side divided by the Hypotenuse
\(sin θ =\frac{Opp}{Hyp}\)

CAH: Cosine of θ equals Adjacent side divided by the Hypotenuse
\(cos θ =\frac{Adj}{Hyp}\)

TOA: Tangent of θ equals Opposite side divided by the Adjacent
\(tan θ =\frac{Opp}{Adj}\)

The Sine, cosine and tangent of some common angles are shown in the table below:

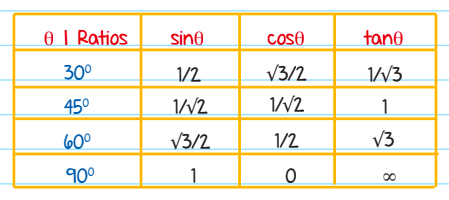
Trigonometry ratios can be expressed in terms of each other as well. The ratio of the sine of θ to the cosine of θ is equal to the tangent of θ:\(tan θ =\frac{sin θ }{cos θ }\)

You may also encounter some inverse trigonometric ratios in an SAT exam.

These are:

• \(Cosecant.\: cosec θ =\frac{1}{sin θ }=\frac{Hypotenuse}{Perpendicular}=\frac{c}{b}\)
• \(Secant.\: sec θ =\frac{1}{cos θ }=\frac{Hypotenuse}{Base}=\frac{c}{a}\)
• \(Contagent.\: cot θ =\frac{1}{tan θ }=\frac{Base}{Perpendicular}=\frac{a}{b}\)

Solved Example 1
Simplify sin(x)cot(x)csc(x)
A. cot(x)
B. sec(x)
C. csc(x)
D. sin(x)

Solution: Write the cotangent and cosecant in terms of sines and cosines.

=sin x \(\frac{1}{tanx}\; \frac{1}{sinx}\)
= \(\frac{1}{tanx}\)
=cot x

The correct answer is A.

Solved Example 2

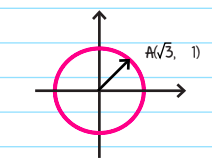
In the xy-plane, O is the center of the circle, and the measure of ∠AOB is \(\frac{\pi }{a}\) radians. What is the value of a?
A. 4
B. 6
C. 8
D. 12

Solution: By the distance formula, the length of radius OA is \(\sqrt{(\sqrt{3})^{2}+1^{2}} = 2\)

Thus Sin(∠AOB) = 1/2 .

Therefore, ∠AOB=30° , which equals to \(30\frac{\left ( \pi  \right )}{180}=\frac{\pi }{6}radians\)

Hence, the value of a is 6. The correct answer is B.

Unit Circle

We know that in a right triangle, an angle cannot be larger than 90° (as the sum of all angles is 180°). So, whenever you’ve been given an angle greater than 90° in a trigonometry problem, draw it in the coordinate plane.

Consider the following angles:

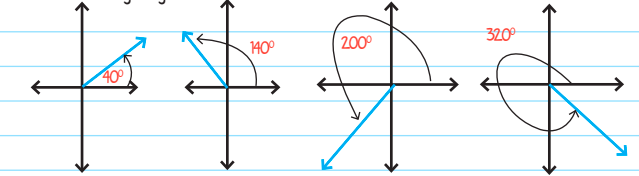
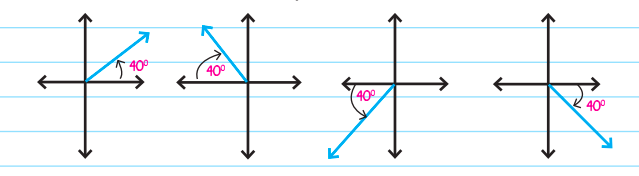
The convention is that an angle in the counterclockwise direction is considered positive. The coordinate plane has four quadrants helpful in dealing with such angles. The angles drawn above are simplified in terms of their own quadrants below:

We can conclude that

• Angle 140° is the same as angle 40°, except that angle 140° is in the second quadrant
• Angles 220° and 320° are the same as angle 40°, except that angles 220° and 320° are drawn in the third and fourth quadrant respectively.

This means, in terms of the trigonometric functions, the magnitudes of 40° and all other drawn angles are the same, but the sign of trigonometric functions are different, depending on the quadrant. The signs of the trigonometric functions, as per the quadrant are given below:

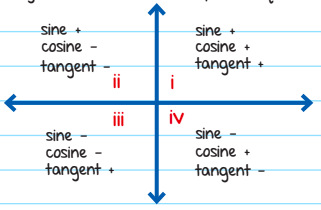
Now, when θ = 30°, sinθ is 0.5.

Now, what value of θ, will sinθ = -0.5?

In the diagram in the previous page, we can see sinθ is negative in the third and fourth quadrant, so there are two possible values of θ i.e.

θ = 180° + 30° & θ = 360° - 30°
θ = 210° & θ = 330°

Solved Example 3 
Which of the following is equivalent to \(Cos\frac{(3\pi )}{10}\) ?
A. - Cos (\(\pi /5\))
B. Sin (\(\pi /5\))
C. - Sin (\(\pi /5\))
D. Sin (\(\pi /5\))

Solution: To answer this question correctly, you need to both understand trigonometry and radians. Sin and cos are related by the equation \(sin \: x=Cos(\frac{\pi }{2}-x)\)

In order to find out what the equivalent to \(Cos (\frac{3\pi }{10})\) is, you need to change \(\frac{3\pi }{10}\) into the form \(\frac{\pi }{2}-x\) to do that, you need to set up an equation: \(\frac{3\pi }{10}=\frac{\pi }{2}-x\)

Then solve for x,
\(\frac{3\pi }{10}=\frac{\pi }{2}=x\)
\(\frac{\pi }{5}=x\)

Therefore, \(cos\frac{(3\pi )}{10}=cos(\frac{\pi }{2}-\frac{\pi }{5})=sin(\frac{\pi }{5})\)

B is the correct answer.

Solved Example 4 
In a right triangle, one angle measures x°, where \(sin\: x^{\circ}-\frac{4}{5}\) . What is cos(90°- x°)

Therefore, cos(90°- x°)= 4/5 or 0.8.

However, you can also solve this problem by constructing a diagram using the given information. It’s a right triangle (which it has to be to use sine/cosine), and the sine of angle x is 4/5.

If \(sin=\frac{Opposite\: Side}{Hypotenuse}\) then the opposite side is 4 long, and the hypotenuse is 5 long:

Since two of the angles of the triangle are of measure x°and 90°, the third angle must have the measure 180° − 90° − x° = 90° − x°

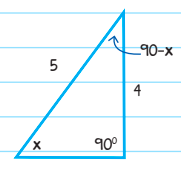
From the figure, cos(90°−x°), which is equal the, is also \(\frac{Adjacent\: Side}{Hypotenuse}\) or 0.8.

Graphing Trigonometric Functions

Every trigonometric function has a certain characteristic graph. The following are those graphs

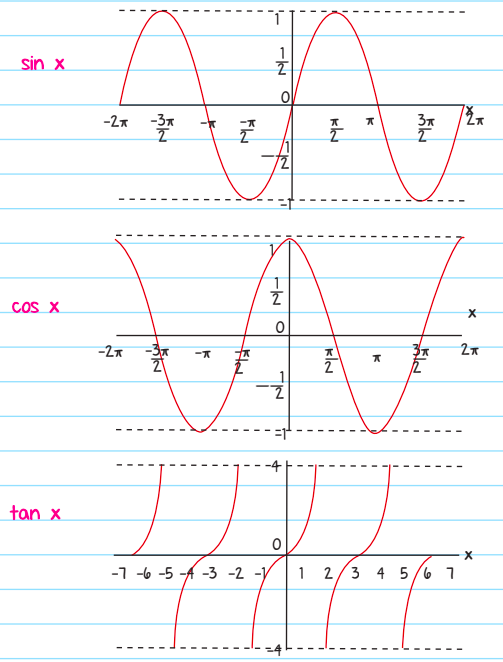
Here are a few points to remember about the above graphs:

• The sin and cos graphs have a few similarities, while the tan graph is a bit different. For example sin and cos graphs repeat after every 2π radians, while tan graph repeats after every π radians.
• The sin and cos graphs extend horizontally, while the tan graph extends vertically.
• The tan has a special graph, as each of its periods is separated by a vertical asymptote. We know tan is a ratio of sin and cos functions. Therefore, vertical asymptote occurs at cos x=0.

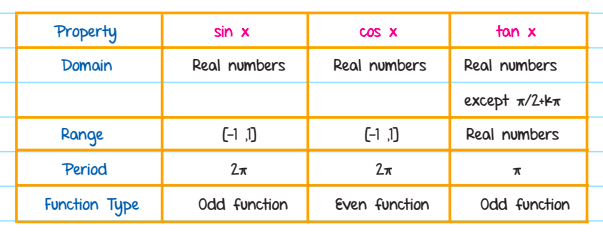
Some other important properties are summarized in the table below:

For y = sin (x),

• There is an amplitude of 1, because the graph extends 1 unit up and 1 unit down.
• The period is 2π because the graph repeats itself every 2π units.

Now, if we have y = 2sin(x),

• The amplitude is increased from 1 to 2,
• The period will remain the same (since nothing is getting multiplied with x).

This graph is shown below.

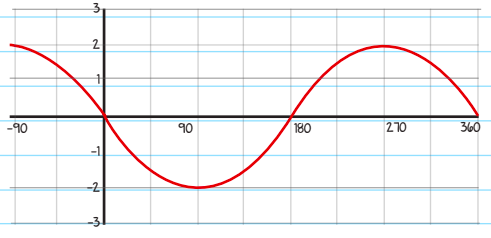
Therefore, we can say the whatever number is multiplied with the trigonometric function will give us the amplitude. If we are looking at y = -sin(x), the graph will be flipped upside down (reflected in x-axis) due to a negative sign:

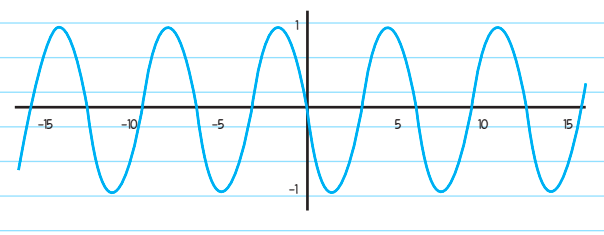
Now, let’s suppose y = sin(3x). Since there is a change in the function internally; therefore, the period will not be the same now (it will be reduced):

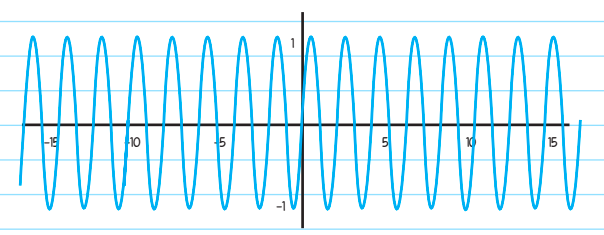
For a function, y=sin(Bx), the formula to calculate period is: \(P=\frac{2\pi }{ \left | B \right |}\)

Therefore, the period of y = sin(3x) is \(\frac{2\pi }{3}\)

The above formula is also true for cos.

For tan, the formula is redefined as: \(P=\frac{\pi }{ \left | B \right |}\)

• If we have a function, \(f\left ( x \right )=cos\left ( x-\frac{\pi }{2} \right )\) then we will shift the graph of f(x)=cos(x) graph to the right by \(\frac{\pi }{2}\) units.
• If we have a function, \(f\left ( x \right )=cos\left ( x \right )+\frac{\pi }{2}\) then we will shift the graph of f(x)=cos(x) graph up by \(\frac{\pi }{2}\) units.

As done in the functions chapter, the general transformed form of a trigonometric function is:
y = A f(Bx+C) + D

where f is any trigonometric function, A is amplitude, B is used to find the period using equation , C can be used to find the phase shift using equation \(\frac{Original\: Period}{\left | B \right |}\) and D is a vertical shift.

Changing the values of A and D bring vertical changes in the graph while changing the values of B and C will bring the horizontal changes.